Summary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functionsThis function, also denoted as exp x, is called the "natural exponential function", or simply "the exponential function" Since any exponential function can be written in terms of the natural exponential as = , it is computationally and conceptually convenient to reduce the study of exponential functions to this particular oneThe natural exponential is hence denoted bySolution for f (x) = 3x5 5x3 Q At 1017 am, you pass a police car at 55 mph that is stopped on the freewayYou pass a second pol A At 1017 am, you are traveling at 55 mph when you pass a police car that is stopped on the freeway
Content Polynomial Function Gallery
F(x)=x^3-4x
F(x)=x^3-4x-F(x)=3 x dan f'(x)=3 x ·ln(3) f(x)=10 2x1 dan f'(x)=2·ln(10)·10 2x1 f(x)=5·($\frac{1}{2}$) x dan f'(x)=5·ln($\frac{1}{2}$)·($\frac{1}{2}$) x f(x)=2 x 24x2 dan f'(x)=ln(2)·2 x 24x2 ·(2x4) Bijzonder geval Als f(x)=e x dan zou je op grond van het bovenstaande verwachten dat de afgeleide f'(x)=e x ·ln(e)=e x wordt en dat kloptI got this answer by looking at x = –3 on the f(x) graph, finding the corresponding yvalue of 1 on the f(x) graph, and using this answer as my new xvalue on the g(x) graph That is, I looked at x = –3 on the f(x) graph, found that this led to y = 1, went to x = 1 on the g(x



Efisd Net Common Pages Displayfile Aspx Itemid
Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?If y=0 , then x 33x 2 =x 2 (x3)=0 so that x=0 and x=3 are the xintercepts There are no vertical or horizontal asymptotes since f is a polynomial See the adjoining detailed graph of f Click HERE to return to the list of problems SOLUTION 2 The domain of f is all xvalues Now determine a sign chart for the first derivative, f' f'(xThe Douglas X3 Stiletto was a 1950s United States experimental jet aircraft with a slender fuselage and a long tapered nose, manufactured by the Douglas Aircraft Company Its primary mission was to investigate the design features of an aircraft suitable for sustained supersonic speeds, which included the first use of titanium in major airframe components
Get an answer for 'Find the complex zeros of the polynomial function Write f in factored form f(x)=x^327 Use the complex zeros to write fSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreShow that the function f(x)=x3,x in R is continuous but not differentiable at x = 3 CBSE CBSE (Science) Class 12 Question Papers 1851 Textbook Solutions Important Solutions 4562 Question Bank Solutions Concept Notes & Videos 725 Time Tables 18 Syllabus
F(x) = x n, f '(x) = n x n–1 Vi ser første på f(x) = x 3 = x x 2 Da begge disse funktioner er differentiable, kan vi benytte produktsætningen, og finder (x 3)' = (x x 2)' = x' x 2 x (x 2)' = 1 x 2 x 2x = 3 x 2 På tilsvarende måde f(x) = x 4 = x x 3 (x 4)' = (xClick here👆to get an answer to your question ️ Domain and range of f(x) = x 3x 3 are respectivelyCalculation f (x) = x 3 9x 2 24 x 14 First, differentiate the given function with respect to x f' (x) = 3x 2 18x24 To find the critical point equate the first derivative to 0 ⇒3x 2 18x24 = 0 ∴ x = 2, 4 Therefore, the critical points of the function are x = 4 and x = 2 Again differentiate the function with respect to x




If F X 2x 3 3x 2 Prove That Fof Is An Identity Function Brainly In



Cubic Functions
Maar wat over meer ingewikkelde functies Bijvoorbeeld, hoe ziet f(x) = (x3) 2 er uit?Click here👆to get an answer to your question ️ The range of the function f(x) = 5 cos x 3 cos ( x pi / 3 ) 4 isPlot f(x)=x^2/(x3) Natural Language;
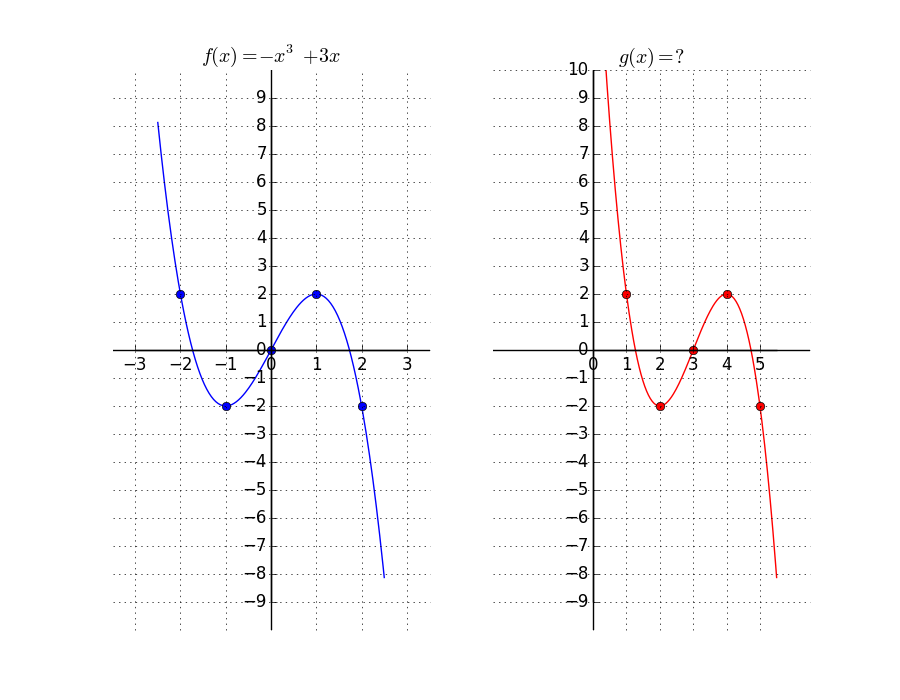



Given The Graph Of The Function F X X3 3x Find Chegg Com




Using Transformations To Graph Functions
Given f(x) = 3/(2 x 2) To find the range of function Explanation So, the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Given, f(x) = 3/(2 x 2) Let this be equal to y, so= 2x 3 x 2 2 The domain of (f g)(x) consists of all xvalues that are in the domain of both f and g In this example, f and g both have domain consisting of all real numbers, therefore (f g)(x) also has domain consisting of all real numbers The Difference of Two FunctionsIs that all correctÉ



Business Calculus



Search Q Parent Functions Tbm Isch
Equations Tiger shows you, step by step, how to Isolate x (Or y or z) in a formula f(x)=(x^(3))^(5)x^(2) and Solve Your Equation Tiger Algebra SolverClick here👆to get an answer to your question ️ If the function f(x) = x^3 e^x/2 and g(x) = f^1(x) ;Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science




Finding Average Rate Of Change Of Polynomials Video Khan Academy




Domain And Range Of F X X 3 X 3 Are Respectively
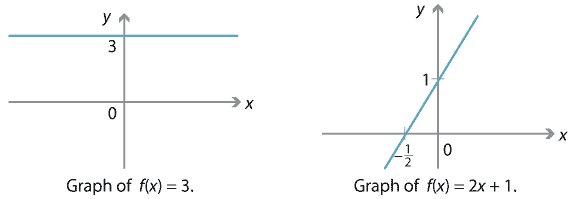
Graph f (x)=3 f (x) = 3 f ( x) = 3 Rewrite the function as an equation y = 3 y = 3 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using theClick here👆to get an answer to your question ️ Prove that the function f(x) = 5x 3 is continuous at x = 0 , at x = 3 and at x = 5F ( x) = 3 x 3 − x 2 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 2 and q divides the leading coefficient 3 One such root is 1 Factor the polynomial by dividing it by x1 Polynomial 3x^ {2}3x2 is not factored since it does not have any rational roots



Math Scene Equations Iii Lesson 3 Quadratic Equations




Show That The Function F X Modulus Of X 3 Is Continuous But Not Differentiable At X 3 Mathematics Topperlearning Com 8yq4x399
If f(x) = x3 \(\frac{1}{x^3}\)then show that f(x) f\((\frac{1}x)\) = 0 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesSimple and best practice solution for F(x)=3x equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Simple and best practice solution for F(x)=x^32x4 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so



Inverse Functions



Curve Sketching
x inRR,x!=3 y inRR,y!=0 >"the denominator of "f(x)" cannot be zero as this" "would make "f(x)" undefined Equating the " "denominator to zero and solving gives the value" "that x cannot be" "solve "x3=0rArrx=3larrcolor(red)"excluded value" "domain is "x inRR,x!=3 (oo,3)uu(3,oo)larrcolor(blue)"in interval notation" "to find the range, rearrange making x the subject" f(xSo applying a function f and then its inverse f1 gives us the original value back again f1 ( f(x) ) = x We could also have put the functions in the other order and it still works f( f1 (x) ) = xX 3 5x 2 = x 2 • (x 5) Step 4 Pulling out like terms 41 Pull out like factors x 2 5x = x • (x 5) Canceling Out 42 Cancel out (x 5) which appears on both sides of the fraction line Dividing exponential expressions 43 x 2 divided by x 1 = x (2 1) = x 1 = x Equation at the end of step 4 fx x = 0 Step 5 Step 6




Question 2 Find The Inverse Of The Function F X Chegg Com




The Relation F Is Defined By F X X 2 0 X 3 3x 3 X 10 The Relation G Is Defined By G X X 2 0 X 2 3x 2 X 10
Merk op dat we f(x) = x 2 (een van de getekende functies hierboven) hebben genomen en x vervangen hebben door (x3) om een nieuwe functie te bekomen Wel, hier zijn enkele "hoofd" regels die ons vertellen wat het effect van deze operaties zijn Redefine the function f(x) = x x in such a way that it could become continuous for x ∈ (0, 2) asked in Limit, continuity and differentiability by Rozy ( 418k points) limitAnd "( f o g)(x)" means "f (g(x))" That is, you plug something in for x, then you plug that value into g, simplify, and then plug the result into f The process here is just like what we saw on the previous page, except that now we will be using formulas to find values, rather than just reading the values from lists of points Given f(x) = 2x



If F X 1 X 2 3x 2 Then What Is The Value Of F X Quora
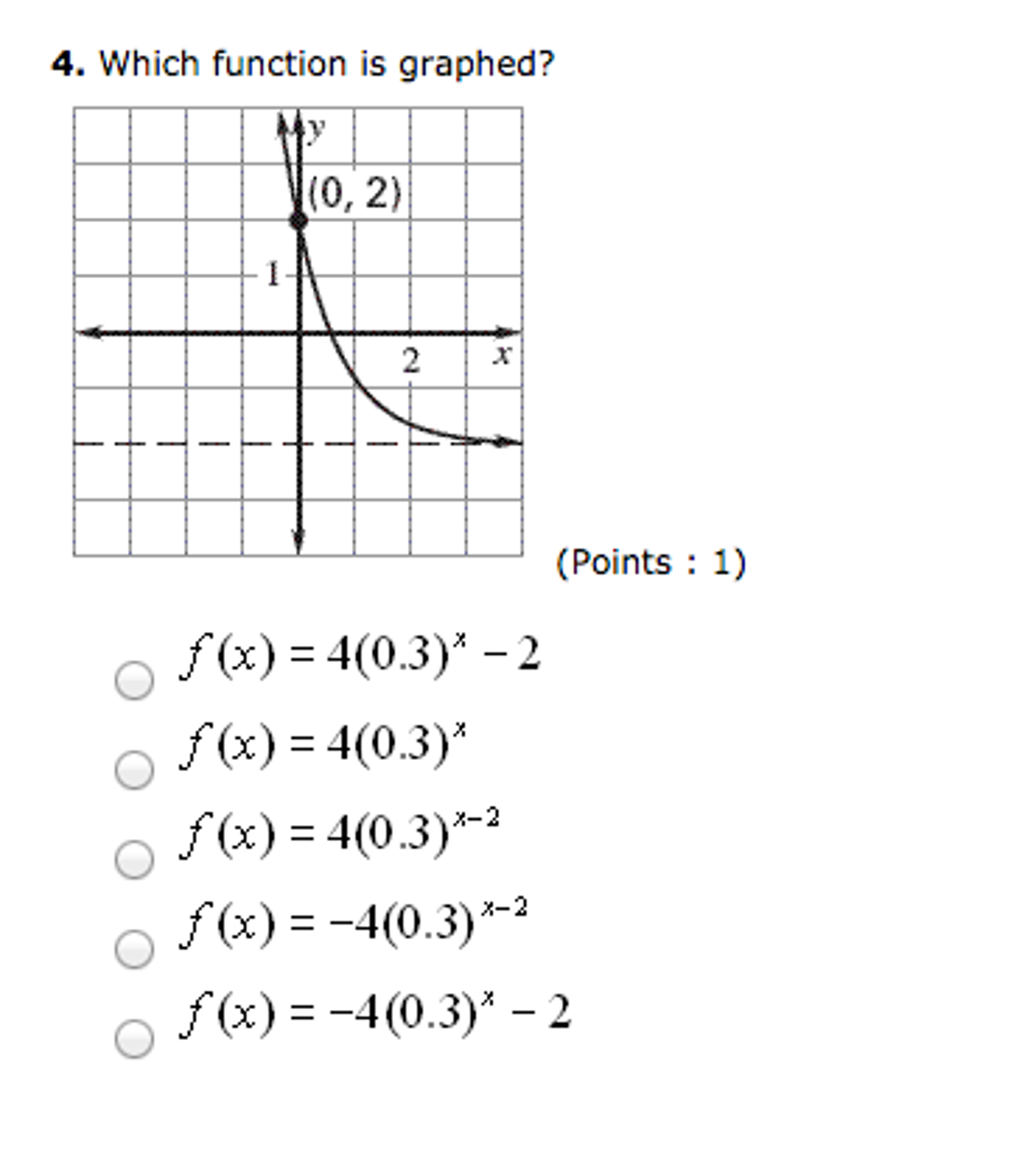



1 Find The Inverse Of The Function F X 3 5 Points Chegg Com
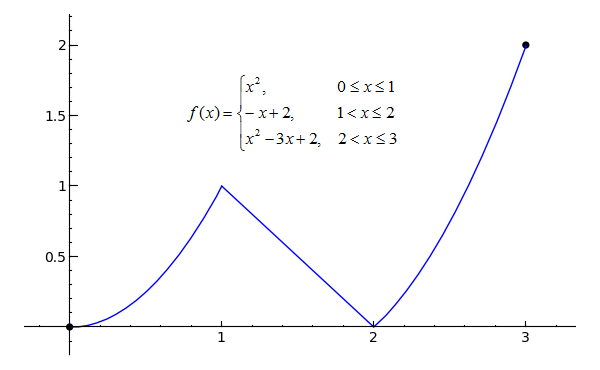
This video shows an example of graphing a polynomial function with a highest degree that is oddSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHence, the name "piecewise" function When I evaluate it at various xvalues, I have to be careful to plug the argument into the correct piece of the function



Www Tamdistrict Org Cms Lib Ca Centricity Domain 3 12 Exam Solutions with detailed solutions Pdf




The Graph Of F X 3 2 X 3 Is Shown Below G X Is A Transformation Of F X How Would You Write The Brainly Com
Then the value of g'(1) is x >= 3 or in interval notation 3, oo) Given F(x) = sqrt(x 3) A function starts out having a domain of all Reals (oo, oo) A square root limits the function because you can't have negative numbers under the square root (they are called imaginary numbers) This means " "x 3 >= 0 Simplifying " "x >= 3 If so, you can read off the derivatives from the Taylor series expansion #3 Calcotron 17 0 Ok, so from the maclaurin series with x^3 substituted I get f (x) = x^3 (x^9/ 3!) (x^15/ 5!) and just from this I can see the 15th derivative of the function is going to be 15!/ 5!




Consider The Function F X X 3 Draw The Graph Of F X Maths Relations And Functions Meritnation Com




Example 4 Show F X X3 3 1 Is Not Continuous At X 0
Math Input NEW Use textbook math notation to enter your math Try it//googl/JQ8NysUse the Graph of f(x) to Graph g(x) = f(x) 3 MyMathlab HomeworkLos uw wiskundeproblemen op met onze gratis wiskundehulp met stapsgewijze oplossingen Onze wiskundehulp ondersteunt eenvoudige wiskunde, prealgebra, algebra, trigonometrie, calculus en




One To One Functions And Their Inverses Read Calculus Ck 12 Foundation




Evaluate Functions For X Given F X 3 Youtube
Please Subscribe here, thank you!!! First Principles > Difference Quotient f'(x)=lim_(h>0)(f(xh)f(x))/h f(x)=x^3 f(xh)=(xh)^3 f'(x)=lim_(h>0)((xh)^3x^3)/h f'(x)=lim_(h>0)((xh)(x^22xhh^2)xGiven the function f (x) as defined above, evaluate the function at the following values x = –1, x = 3, and x = 1 This function comes in pieces;



On Dividing The Polynomial F X X3 5x2 6x 4 By A Polynomial G X The Quotient And Remainder Are X 3 And 3x 5 Respectively Find The Polynomial G X Snapsolve
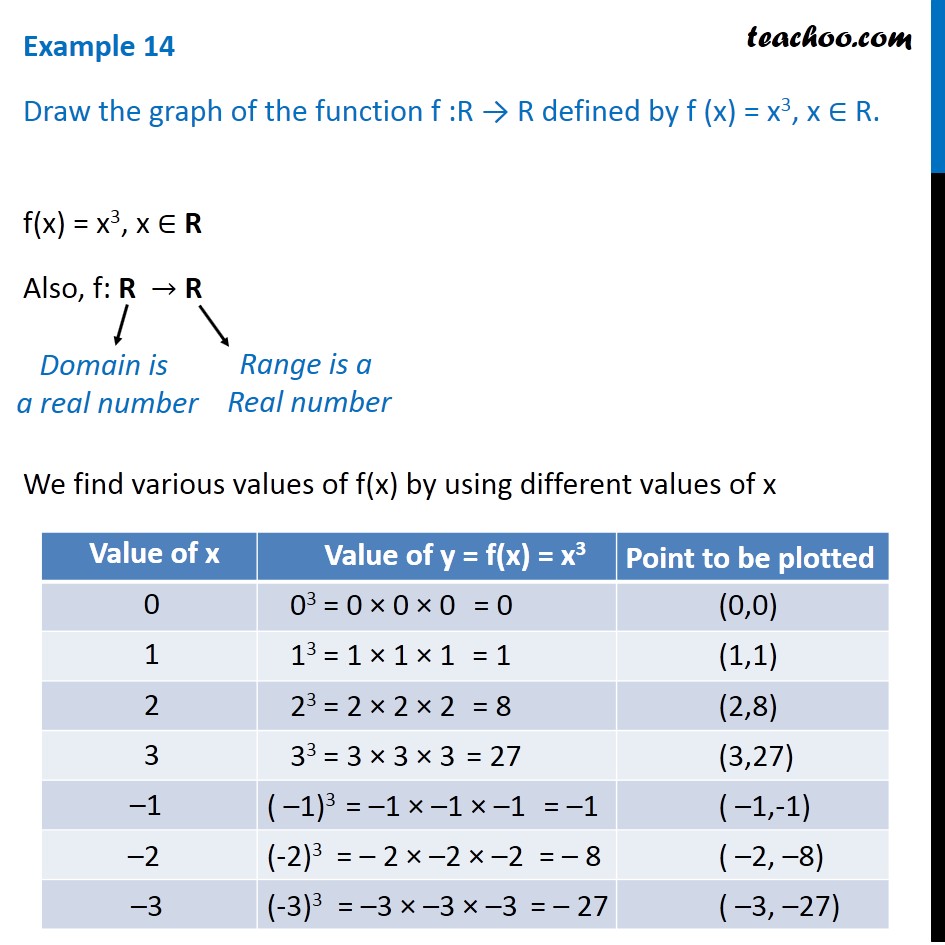



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11
1 If the function is math\frac 32 x^2/math, then like others have pointed out — the maximum exists for mathx=0/math and there is no lower bound Thus the range is mathSimple and best practice solution for f(x)=x^3x30 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, soAnswer to Find the derivative of f(x) = (x csc(x^3 3))^(3) By signing up, you'll get thousands of stepbystep solutions to your homework



Solutions Math 1314 College Algebra



Can You Sketch The Graph Of F X 2x 2 X 3 2x 3 And Give Its Domain Intercepts Asymptotes And Range Quora
X = −1 are not in the domain of f(x) since they are zeros of Q(x) However, if x ≠ 1 we can cancel the factor x − 1 in the numerator and denominator as, Notice that f(x) and agree everywhere except at the point x = 1 (since x = 1 is not in the domain of f(x), but is in the domain of g(x))Domain of f(x) = x/(x^21) Natural Language;Example 2 f(x) = x n where n = 1, 2, 3 d In this example we answer the question "What is x n ?" Once we know the dx answer we can use it to, for example, find the derivative of f(x) = x4 by replacing n by 4




If F X X 3 Find The Value Of F 5 F 1 5 1
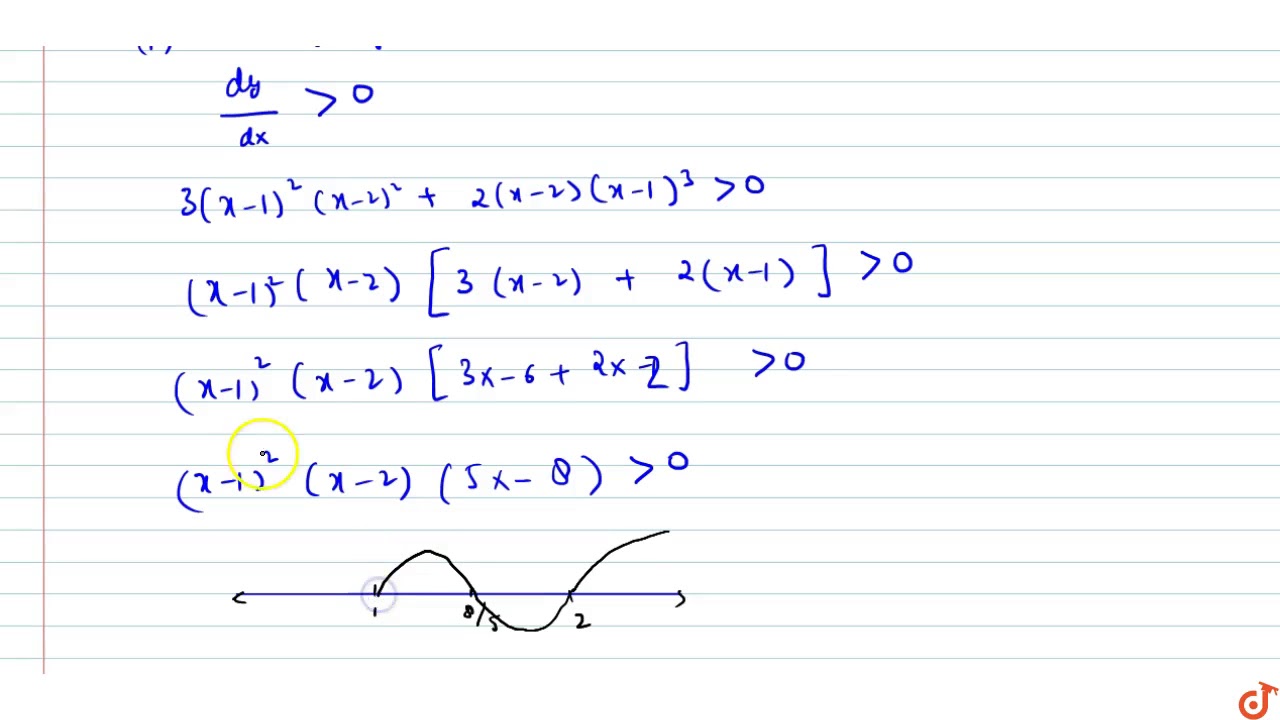



Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube
Is it math\frac 32 x^2/math or math\frac{3}{2x^2}/math? Ex 51, 7 Find all points of discontinuity of f, where f is defined by 𝑓(𝑥)={ (𝑥3, 𝑖𝑓 𝑥≤−3@ −2𝑥, 𝑖𝑓−3




Maclaurin Series For F X 1 1 X 3 Math Calculus Showme
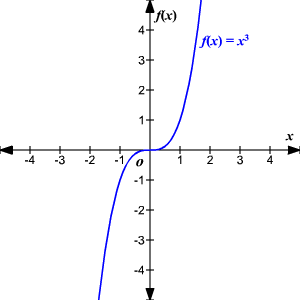



Even Odd Functions



Sage Calculus Tutorial Continuity
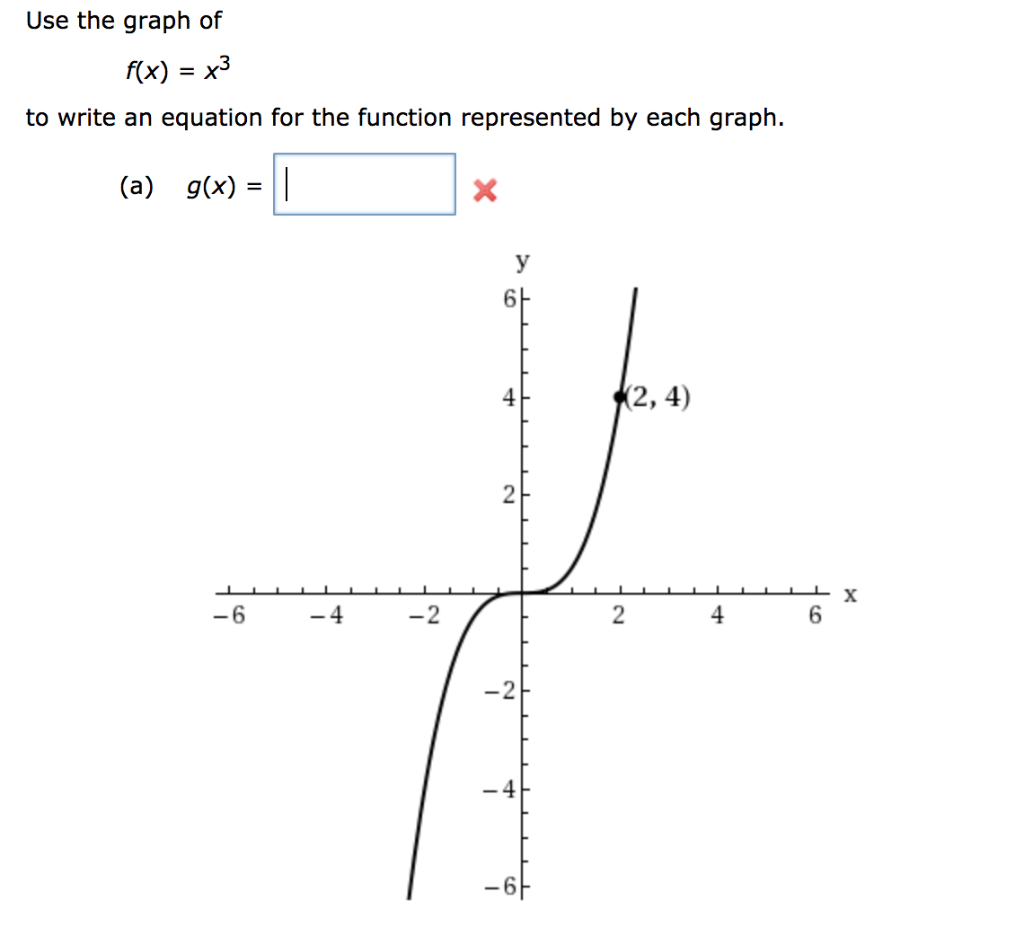



Use The Graph Of F X X3 Equation For The Chegg Com




How Do You Find F X Using The Limit Definition Given F X X 2 1 2x 3 Socratic




Example 8 Find Derivative Of F X 3 At X 0 X 3 Examples



Prove That F X X 2 X 6 X 3 When X 3 5 When X 3 Is Continuous At X 3 Sarthaks Econnect Largest Online Education Community




Example 8 Show F X X3 3x2 4x Is Strictly Increasing




If F X 3 X 1 X 2 3x Find F 0 Maths Continuity And Differentiability Meritnation Com




Function Definition Types Examples Facts Britannica



If The Function F Given By F X X 3 3 A 2 X 2 3ax 7 For Some A R Is Increasing In 0 1 And Decreasing In 1 5 Sarthaks Econnect Largest Online Education Community
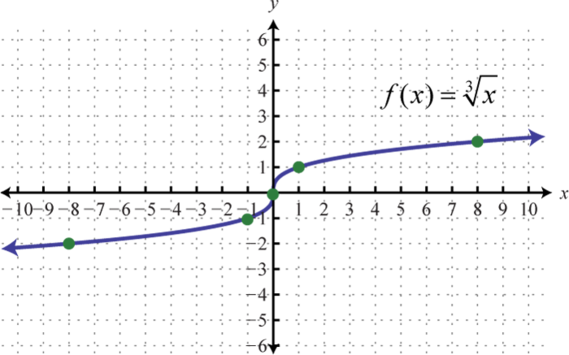



Graphing The Basic Functions



Solution Graph F X X 3 2 Include All Intercepts And The Vertex I Am Not Sure How To Do The Absolute Value Signs On Here But They Should Go Where The Parentheses Are Thank You
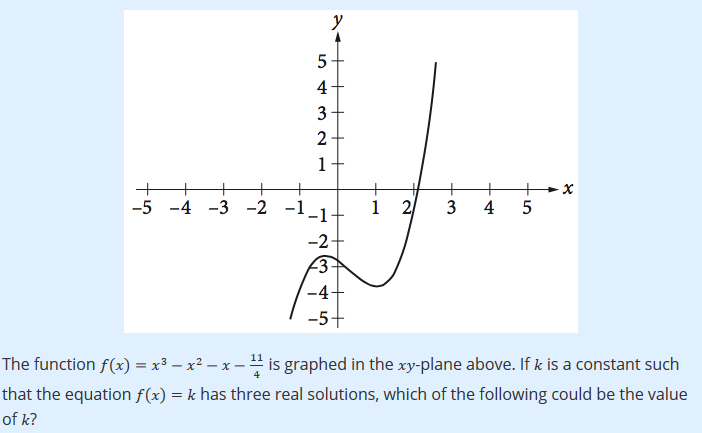



4 2 4 The Function F X X3 X2 X 11 Is Graphed In Chegg Com




Which Is The Graph Of F X 3 2 1 3 X Brainly Com
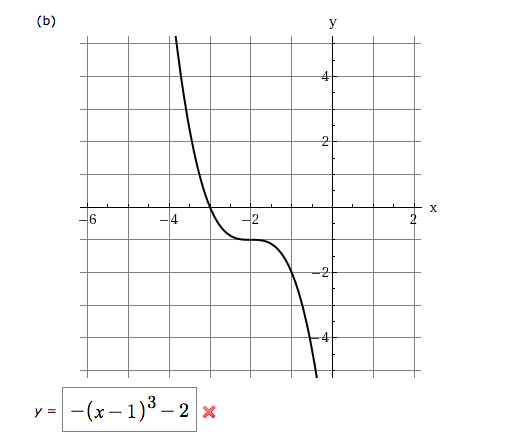



Use The Graph Of F X X3 To Write An Equation For Chegg Com




Content Polynomial Function Gallery




Find The Period Of F X With F X F Y F X Y F X Y Mathematics Stack Exchange




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic



F X F X 2 F X 2




The Table Represents The Function F X What Is F 3 Home Work Help Learn Cbse Forum



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf




Misc 18 If F X X 3 Show That F X Exists And Find It



What Is The Inverse Of X 3 X Quora
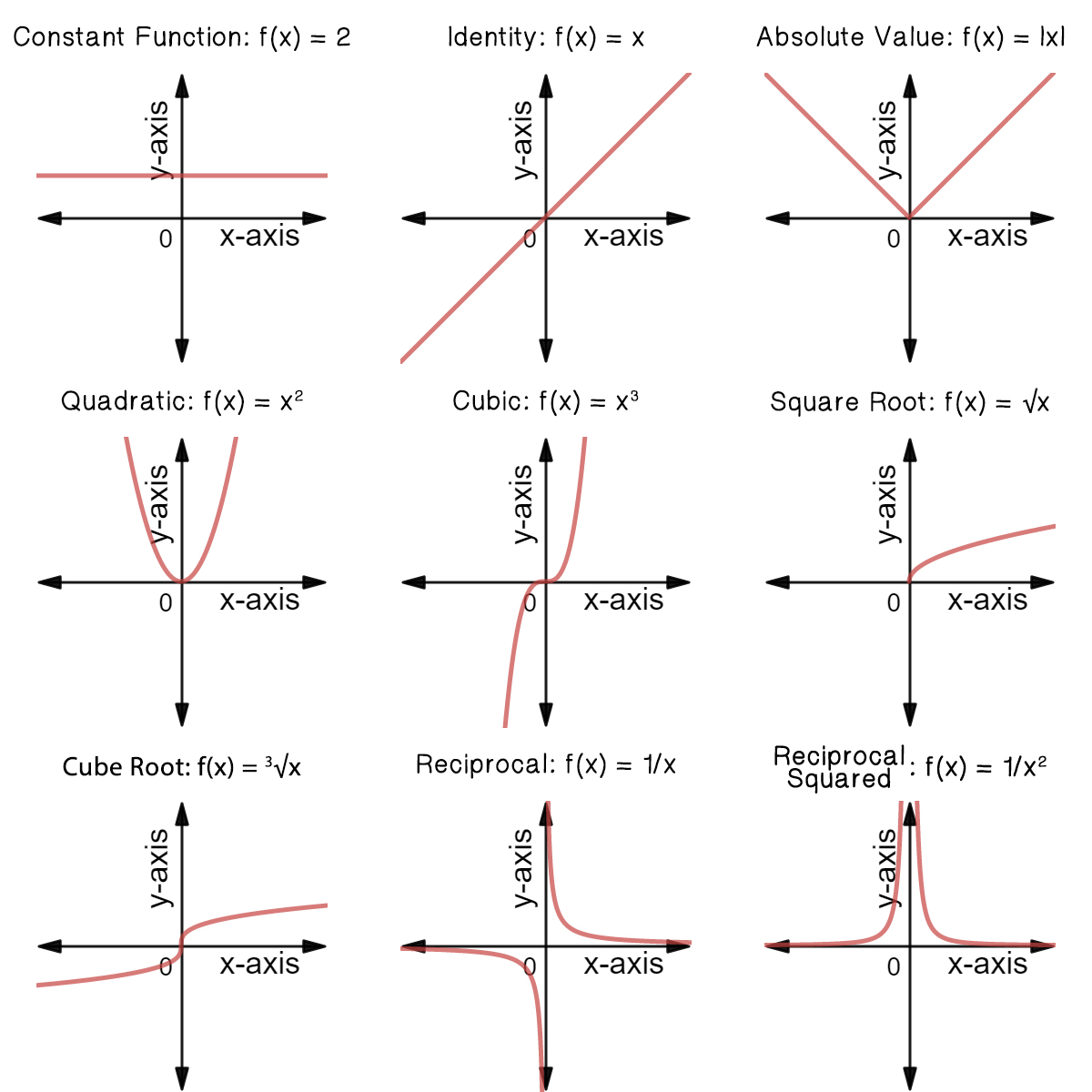



Classifying Common Functions Expii



Biomath Functions



Efisd Net Common Pages Displayfile Aspx Itemid
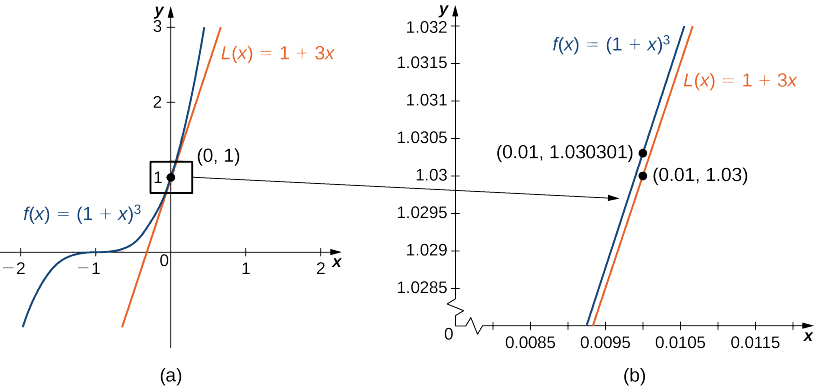



4 2 Linear Approximations And Differentials Mathematics Libretexts



Mhf4u1 P1 8 2 Main
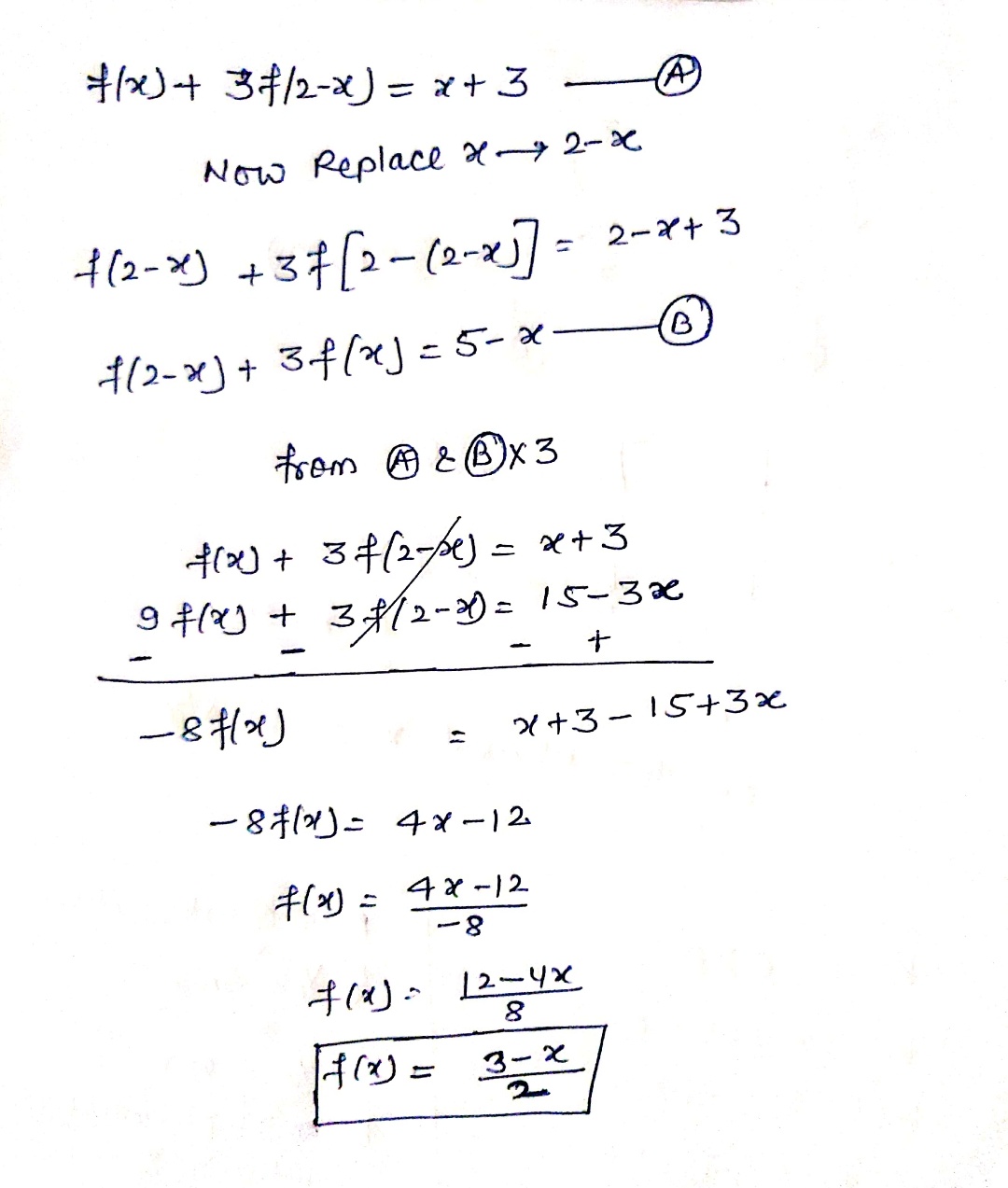



F X 3 F 2 X X 3 Find F X



How To Find F 2 If F X 2 5x 4 X 3 Quora
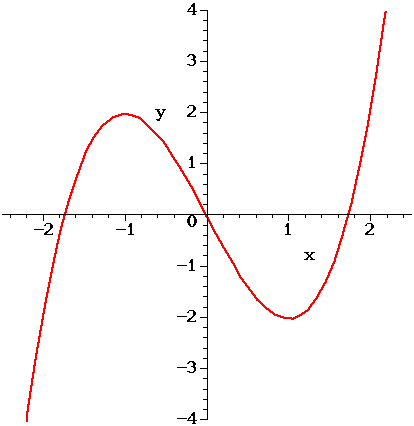



1 The Figure Above Shows The Graph Of F X X 3 Chegg Com




A Function Is Defined By F X 3 2x Find X Such That F X To The Power 2 F X The Whole Square Brainly In




How Do You Find The Derivative Of F X 3 X 2 Using The Limit Definition Socratic



Www Math Utah Edu Wortman 1050 Text If Pdf
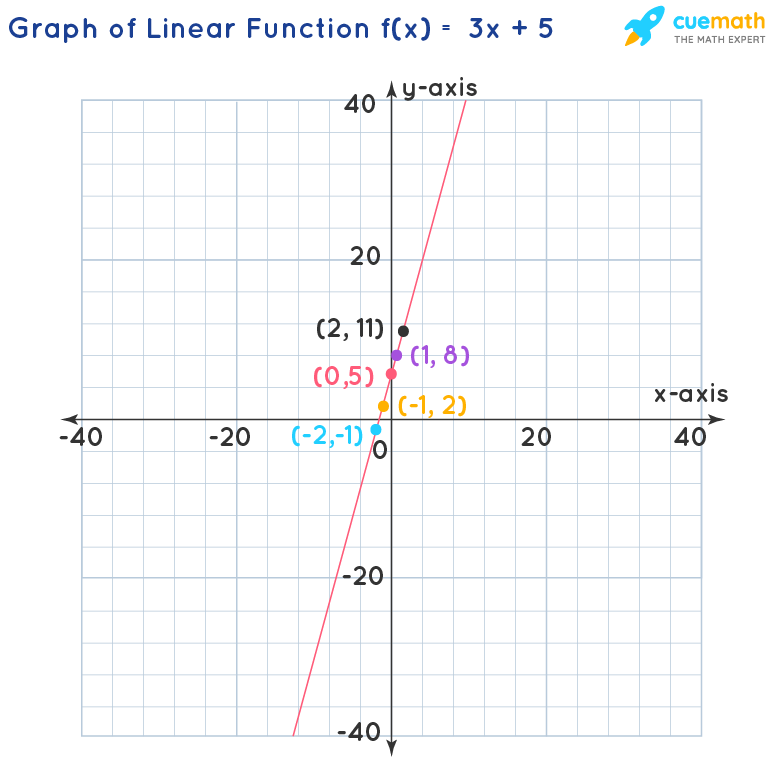



What Are The Domain And Range Of The Function F X 3 X 5 Solved




B Let F X 2x 3 G X 3x 4 And H X 4x For X R Where R Is Set Of Real Numbers Find Gof Fo8 Foh And Goh Answer Discrete Structure




19 Find The Inverse Function For F X X 3 4 Youtube



Examine The Continuity Of The Function F X X3 2x2 1 At X 1 Studyrankersonline




Answered Express The Function In The Form F G 1 Bartleby




What Is The Difference Between F X X 2 1 And F X X 3 1 When Finding The Inverse Mathematics Stack Exchange




If F X X 1 X 2 X 3 Then A Maximum Value Of F X Is 3 If X In 2 3 B Maximum Youtube
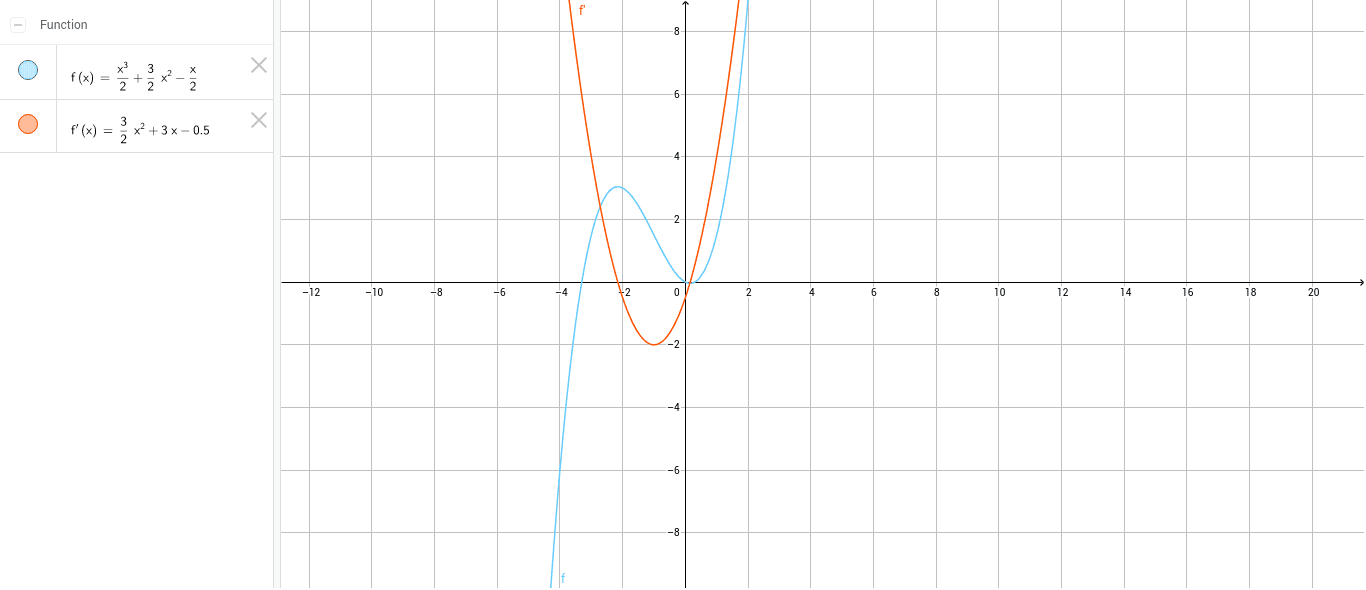



F X X 3 2 3 2x 2 X 2 Geogebra
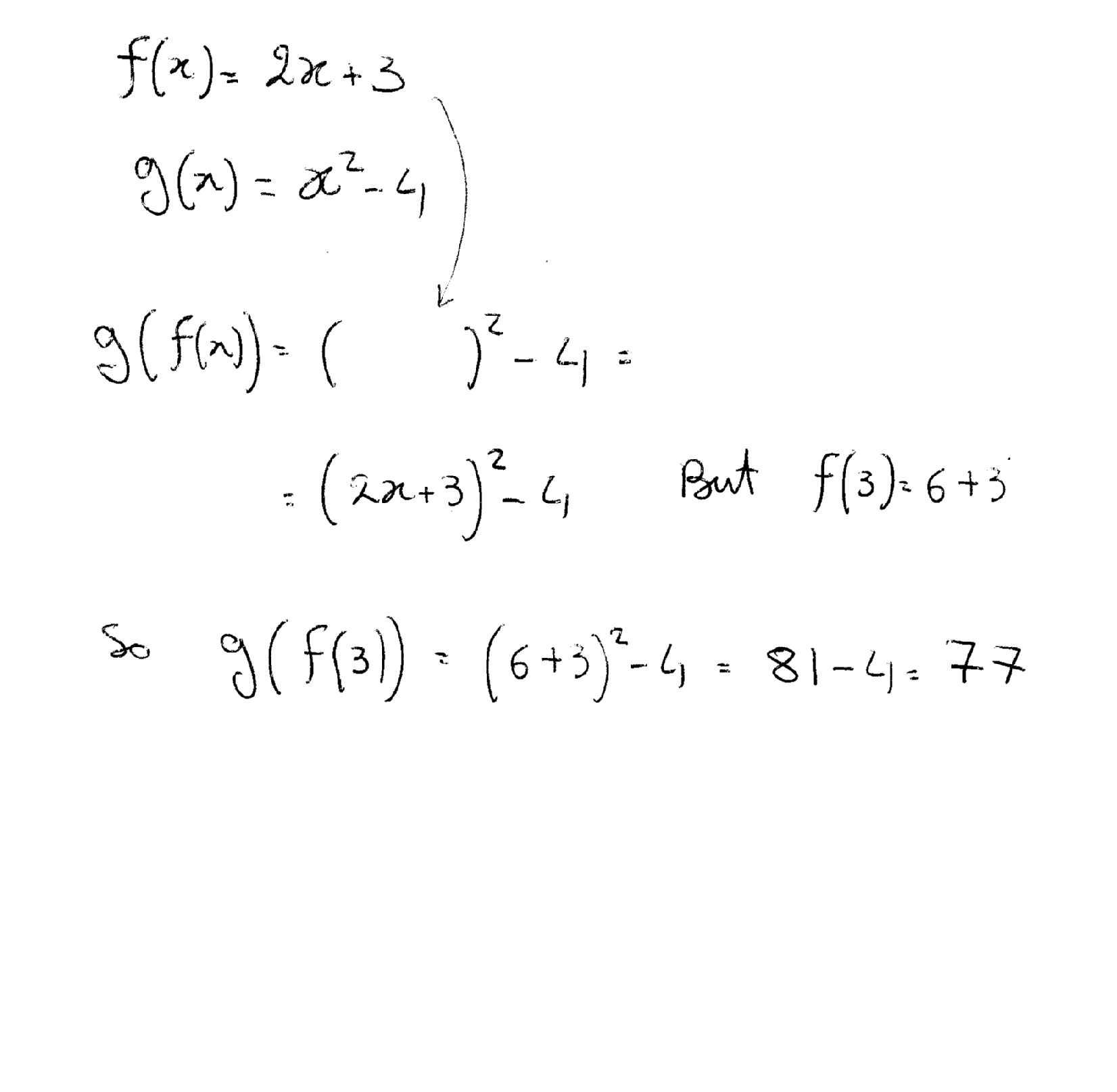



Let F X 2x 3 And G X X 2 4 And H X X 3 2 How Do You Find G F 3 Socratic



F X X Graph
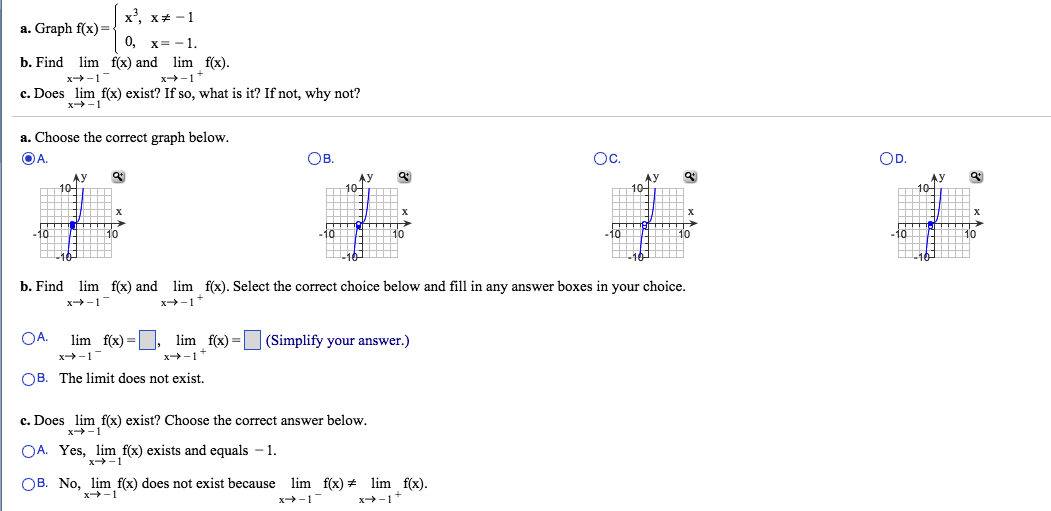



Graph F X X3 X 1 0 X 1 Find F X And Chegg Com




Given That F X 2 X 4 And G X 3 X 5 Find Gf 3 With Noob Like Steps Please I Need A Really Clear Working To Fully Understand Thanks 3 Socratic



Critical Points




If F X X 2 2x 7 Find F 3



If F X 1 2x 3 Find F 3 Youtube




Verifying Inverse Functions By Composition Not Inverse Video Khan Academy




Differentiation F X X 3 2x 2 3x 5 F X 3x 2 4x 3 F 1 3 X X 1 3 3 4 If F X X 3 2x 2 Ppt Download




If F X 3 X 1 X 2 3x Find F 0



Solution The Function F Given By F X 2x 3 3x 2 12x Has A Relative Minimum At X A 1 B 0 C 2 D 3 Amp 8730 105 4 E 3 Amp 8730 105 4



More Differentiation By First Principles




How Is F 2 Equal To 3 In F X X 2 4 X 2 Quora
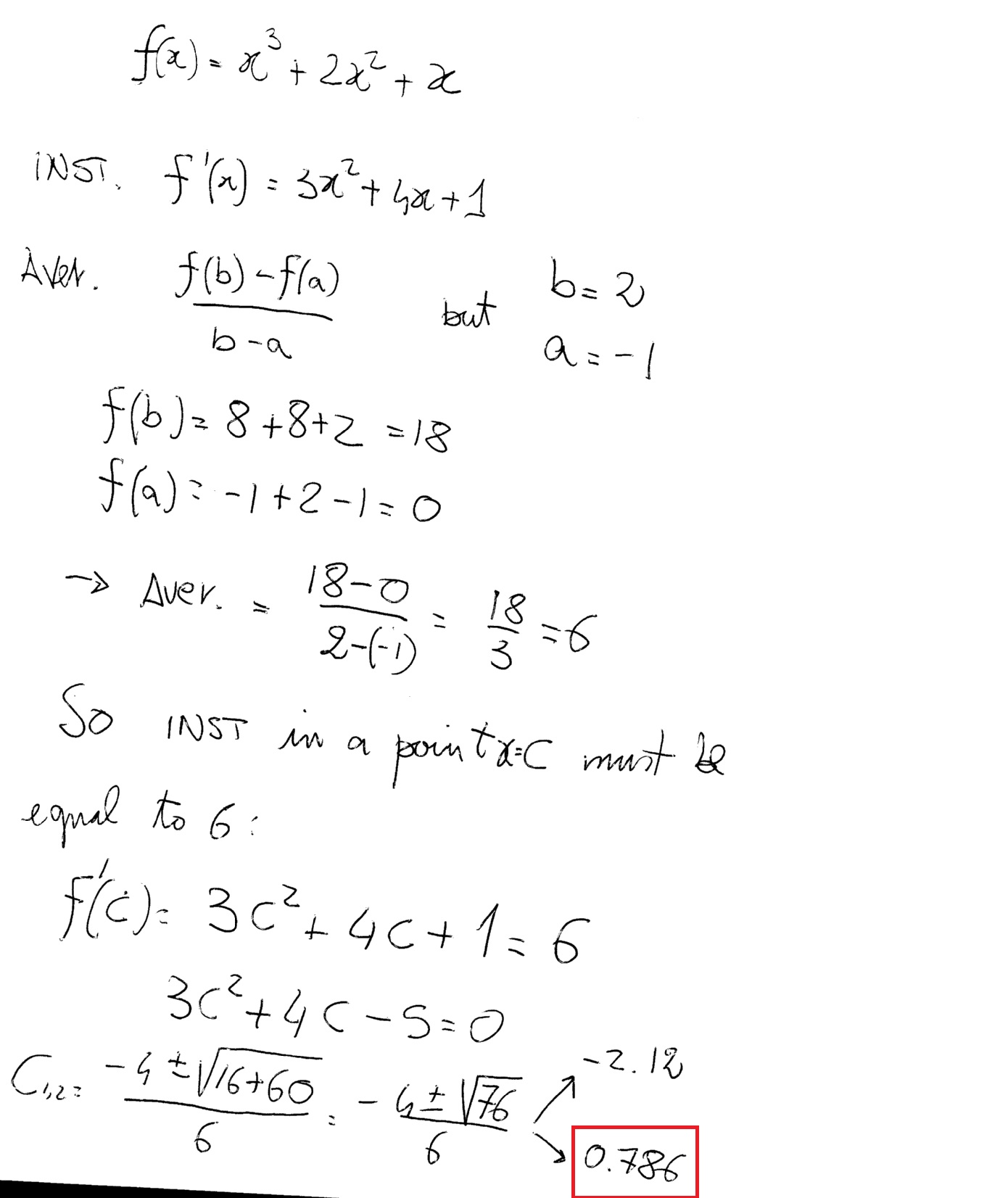



If F Is Defined By F X X 3 2x 2 X How Do You Find The Value Of X When The Average Rate Of Change Of F On The Interval X 1 To X
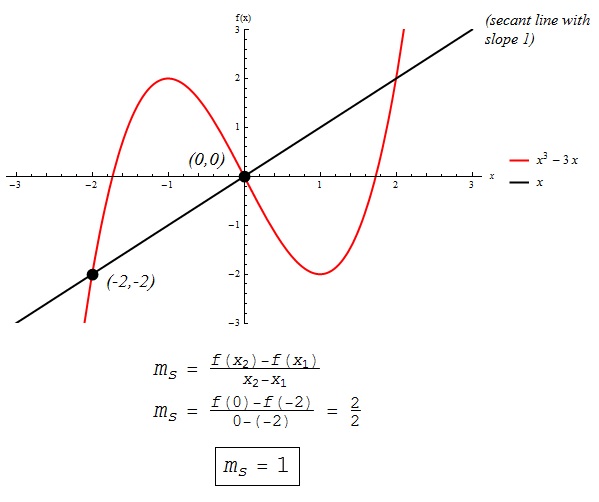



Find The Average Rate Of Change Of F X X 3 3x From X1 2 To X2 0 Enotes Com



Draw The Graph Of The Function F R R Defined By F X X 3 Find Its Domain And Range Sarthaks Econnect Largest Online Education Community



Manipulating Graphs




F X X 3 X 2 16 X X 2 2 X 2k K X 2 Find The Value Of K So That The Followi Youtube
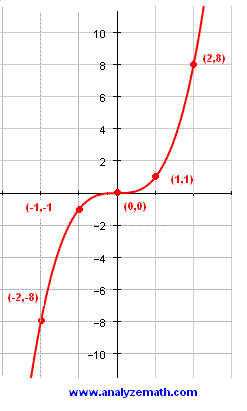



Graphing Cubic Functions



Http Media Collegeboard Com Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf
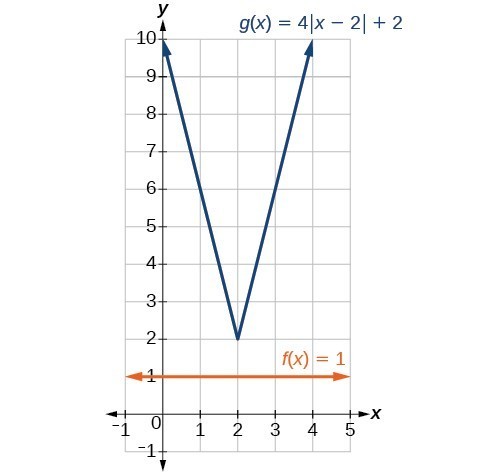



Solve An Absolute Value Equation College Algebra
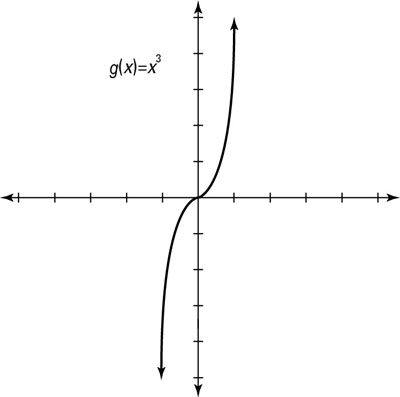



How To Graph Parent Functions Dummies




If F X 9 X Upon 9 X 3 Then F X F 1 X Brainly In




Transformations Cubic Polynomials



Http Www Mpsaz Org Rmhs Staff Lxcoleman Trig Test Practice Files Review Chapter 3 Notes Solutions Pdf



More Differentiation By First Principles



Search Q X 3d3 Graph Tbm Isch
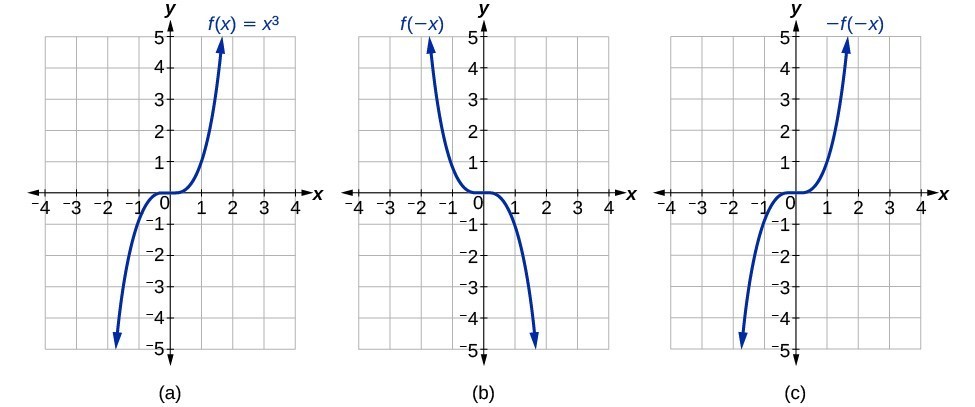



Determine Whether A Function Is Even Odd Or Neither From Its Graph College Algebra
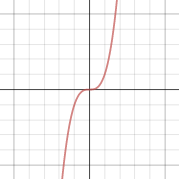



F X X 3




F X X 3 2 And G X 2x 3 Find Fog And Gof Is F Inverse G Maths Relations And Functions Meritnation Com



Search Q X 5e4 Graph Tbm Isch




Maximum Value Of Function F X Frac X 4 X 2 X 6 2x 3 1 When X 1 Mathematics Stack Exchange




Ex 1 3 4 If F X 4x 3 6x 4 Show That Fof X X



0 件のコメント:
コメントを投稿